Orienteering [B]

Memory limit: 32 MB

Byteman is organizing an orienteering competition. Participants will be given a map that indicates checkpoints, and they are to visit each one of them in a given order. By the traditions of Byteland, the route has to be a closed loop. An appropriate area has been found and the route planned accordingly. However, the starting point, which will be the first and the last to visit, and the race direction are yet to be chosen.

Byteman decided that every part of the race should not be more difficult than a previous one. He walked the entire way noting stage difficulty between every two consecutive checkpoints as positive integer numbers. The higher the number is, the more difficult the corresponding part of the route. Your task is to check whether there exist such starting point and race direction, that Byteman's constraint is satisfied.

Input

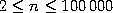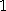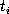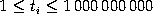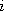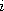The first line of the standard input contains an integer () denoting the number of all checkpoints on the route. The checkpoints are numbered from to . In the second line, there is a sequence of integers (), in which -th number describes difficulty of the stage between checkpoints and 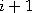, except for 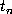, which denotes the difficulty of the stage between checkpoints and .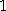

Output

In the first line of the standard output your program should output "TAK" (meaning yes, without the quotes), if there is a starting point and race direction satisfying Byteman's condition, and "NIE" (meaning no) otherwise.

Example

For the input data:

5
3 8 10 1 3

the correct result is:

TAK

and for the input data:

4
5 6 5 6

the correct result is:

NIE

Explanation: In the first example Byteman may set the starting point in the fourth checkpoint (i.e., at the end of the stage with difficulty 10) and the competitors can start the race going towards the third checkpoint. The consecutive stages on their way will have difficulties equal to 10, 8, 3, 3 and 1. In the second example no solution exists.

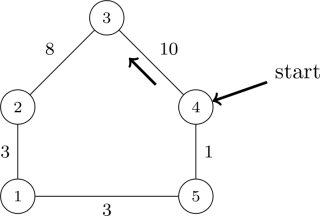
The route of the orienteering competition in the first example. The circles contain the numbers of checkpoints, and the numbers next to the edges represent the difficulties of the stages in the route. The arrows in the picture show valid starting point and race direction.

Task author: Jakub Lacki.